整体逻辑比较简单，适合对Python有一定了解，并对OR-Tools求解器感兴趣的同学，作为简单入门案例。

一、摘要

最近在浏览V2EX站时发现一个求助帖，求助：用 Python 安排监考–让科技来拯救一下手搓党，感兴趣的可以看下原贴。

主要是想通过编程代码方式，完成对监考老师的分配工作。

目前手动解决方法：（有时需要 2 次才能排出监考表）

1. 先根据场次限制，制作出所有老师的监考次数。
2. 根据特殊要求先安排必监考科目和考场和不监考科目和考场的老师，逐个复制粘贴到监考表。
3. 单科目一个人不能重复出现。还需要考虑到能一天安排安排的就别分散安排。
4. 统计老师名单中所有老师在各科中出现的次数以及总的监考场次。然后手动逐一调整。

因为最近也在做类似排产排程相关内容，也有了解过OR-Tools的基本使用。这跟官方的一个示例很接近: 员工日程安排。

二、分析

即需求分析，看下原始数据。

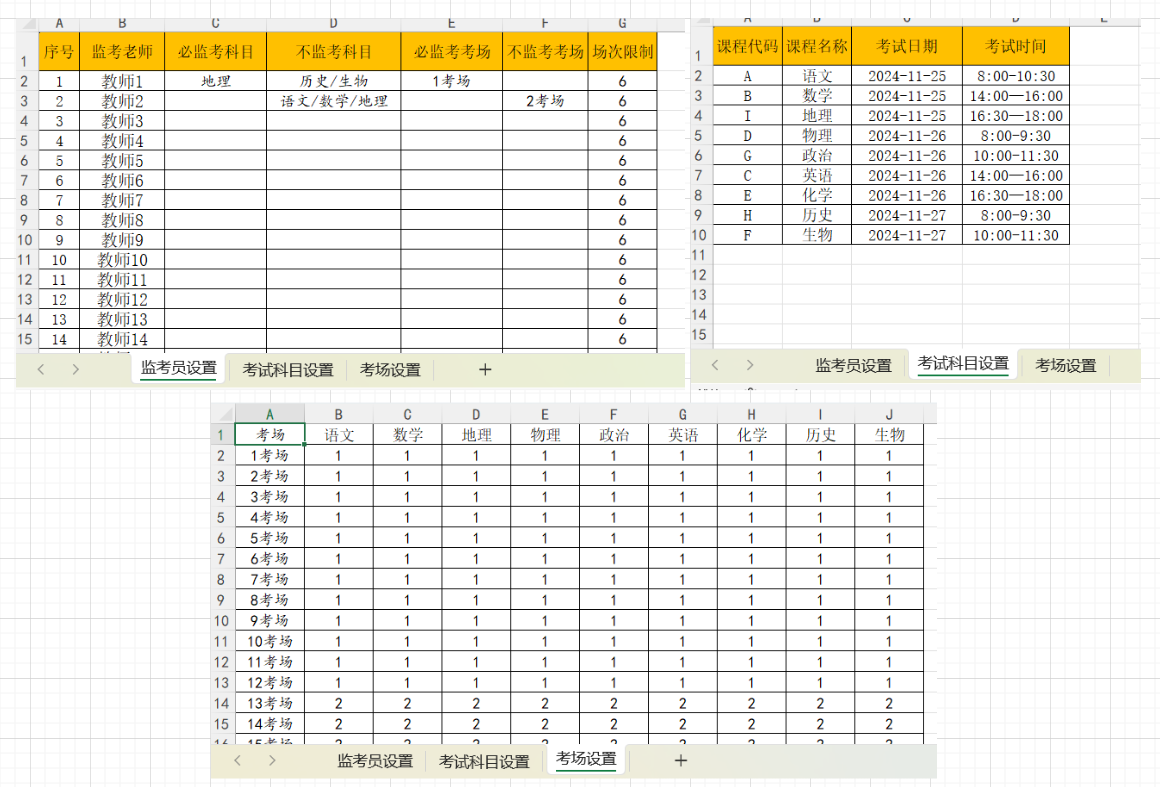
主要有三个维度数据。

监考员设置
- 必监考/不监考科目
- 必监考/不监考考场
- 场次限制
考试科目设置
- 日期
- 时间
考场设置
- 不同科目所需监考老师数量

三、建模

本着学习及方便阅读的方式，咱们将建模做的可读性强一些。

3.1 对象建模

class Teacher(object):

    def __init__(self, arr: ndarray[7]):
        self.no = arr[0]
        self.name = arr[1]
        self.s_y = arr[2]
        self.s_n = arr[3]
        self.r_y = arr[4]
        self.r_n = arr[5]
        self.times_limit = int(arr[6])


class Subject(object):

    def __init__(self, arr: ndarray[4]):
        self.code = arr[0]
        self.name = arr[1]
        self.date = arr[2].date().strftime('%Y%m%d')
        self.time = arr[3]

    @property
    def apm(self):
        """
        判断下当前时间是 AM、PM
        :return:
        """
        if '-' in self.time:
            stime, etime = self.time.split('-')
        else:
            stime, etime = self.time.split('—')
        if int(etime.split(':')[0]) < 13:
            return 'AM'
        if int(stime.split(':')[0]) > 13:
            return 'PM'
        raise Exception('time range error')


class Room(object):
    serials = []

    def __init__(self, arr: ndarray[10]):
        self.name = arr[0]
        self.nums = arr[1:]

将输入的Excel数据进行结构化处理，转换成对象加载到内存中，供后续代码使用。

3.2 逻辑建模

该问题属于CP(约束优化)问题。CP 基于可行性（找到可行的解决方案）而非优化（找出最佳解决方案），并且侧重于约束和变量，而非目标函数。事实上，CP 问题可能甚至没有目标函数 - 目标是通过为问题添加约束条件，将大量可能的解决方案缩小为更易于管理的子集。

3.2.1 初始变量

这种问题，通常会设置类似{'X1_Y1_Z1': True}这种结构的字典，来表示X/Y/Z在某个条件下是否可行。

对于当前问题，我们可以设置如subject_语文_room_1考场_teacher_教师1来表示，当前是否为可行解。若为True则表示: 教师1 在语文考试时被安排在1考场

同时，我们还需考虑目标函数，即：尽量将老师的监考任务安排的集中一些。换句话说，就是尽量将有任务的上午、下午时间段都排满。

这样的话，我们可以设置teacher_教师1_date_20241201_apm_AM来表示: 教师1 在20241201日上午是否有安排监考。

于是，我们就将老师的监考时间段维度细化到了上、下午，那么目标函数可以设置为: 所有老师的监考时间段最少。

# 2. 创建变量
inv_schedule = {}
teacher_date = {}
for s in subjects:
    for r in rooms:
        for t in teachers:
            var_name = f'subject_{s.name}_room_{r.name}_teacher_{t.name}'
            inv_schedule[(s.name, r.name, t.name)] = model.new_bool_var(var_name)
    for t in teachers:
        var_name = f'teacher_{t.name}_date_{s.date}_apm_{s.apm}'
        teacher_date[(t.name, s.date, s.apm)] = model.new_bool_var(var_name)

3.2.2 约束设置

某老师在某个时间段(科目)，最多只能在某个教室出现1次。

# 同一科目，同一个老师，最多只能出现一次
for s in subjects:
    for t in teachers:
        model.add_at_most_one(inv_schedule[(s.name, r.name, t.name)] for r in rooms)

某科目下，当前教室，必须出现特定数量的老师。

# 同一科目 某教室，只能出现指定数量老师
for s in subjects:
    for r in rooms:
        idx = r.serials.index(s.name)
        nums = r.nums[idx]
        model.add(sum(inv_schedule[(s.name, r.name, t.name)] for t in teachers) == nums)

某老师限制场次数量 (最多监考次数)

# 同一老师限制最长场次
for t in teachers:
    model.add(sum(inv_schedule[(s.name, r.name, t.name)] for s in subjects for r in rooms) <= t.times_limit)

限制老师的必监考/不监考科目。只需要限制是否允许出现 subject_语文_room_1考场_teacher_教师1 这种序列即可，但这块要统计所有的room教室。

# 限制 必监考科目/不监考科目
for t in teachers:
    # 必监考科目
    if isinstance(t.s_y, str):
        sys = t.s_y.split('/')
        for sy in sys:
            model.add_at_least_one(inv_schedule[(sy, r.name, t.name)] for r in rooms)
    # 不监考科目
    if isinstance(t.s_n, str):
        sns = t.s_n.split('/')
        for sn in sns:
            model.add(sum(inv_schedule[(sn, r.name, t.name)] for r in rooms) == 0)

限制必监考/不监考教室。

这块可能会有些问题，就是限制必监考时，是限制只能？还是必须在必监考教室监考一次？

# 限制 必监考教室/不监考教室
for t in teachers:
    # 必监考教室
    if isinstance(t.r_y, str):
        rys = t.r_y.split('/')
        for ry in rys:
            # 逻辑1: 这个老师至少在这个教室一次
            # model.add_at_least_one(inv_schedule[(s.name, ry, t.name)] for s in subjects)
            # 逻辑2: 这个老师只能在这个教室
            model.add(
                sum(inv_schedule[(s.name, r.name, t.name)] for s in subjects for r in rooms if r.name != ry) == 0)
    # 不监考教室
    if isinstance(t.r_n, str):
        rns = t.r_n.split('/')
        for rn in rns:
            model.add(sum(inv_schedule[(s.name, rn, t.name)] for s in subjects) == 0)

工作时间约束。教师工作时间粒度与监考安排，会通过科目和科目的上下午相互关联影响。

# 工作时间
for t in teachers:
    for s in subjects:
        model.add_bool_or([inv_schedule[(s.name, r.name, t.name)].Not() for r in rooms]).only_enforce_if(
            teacher_date[(t.name, s.date, s.apm)].Not())
        model.add_bool_or([inv_schedule[(s.name, r.name, t.name)] for r in rooms]).only_enforce_if(
            teacher_date[(t.name, s.date, s.apm)])

3.2.3 目标函数

只需要保证所有老师最小工作粒度(上、下午)数量最少即可。

# 4. 定义目标函数
# 尽量不要分散排 -> 每个老师工作的日期(date+AM/PM)数量最少 -> 全部老师工作日期最少
model.minimize(sum(teacher_date[(t.name, s.date, s.apm)] for s in subjects for t in teachers))

3.3 求解

# 1. 初始化模型
model = cp_model.CpModel()

# 5. 添加求解器
solver = cp_model.CpSolver()
status = solver.Solve(model)

# 6. 处理结果
result = []
if status == cp_model.OPTIMAL:
    for s in subjects:
        for r in rooms:
            for t in teachers:
                if solver.boolean_value(inv_schedule[(s.name, r.name, t.name)]):
                    print(f'科目: {s.name}, 教室: {r.name}, 老师: {t.name}')
                    result.append((s.name, r.name, t.name))

else:
    print('no solution')

四、结果

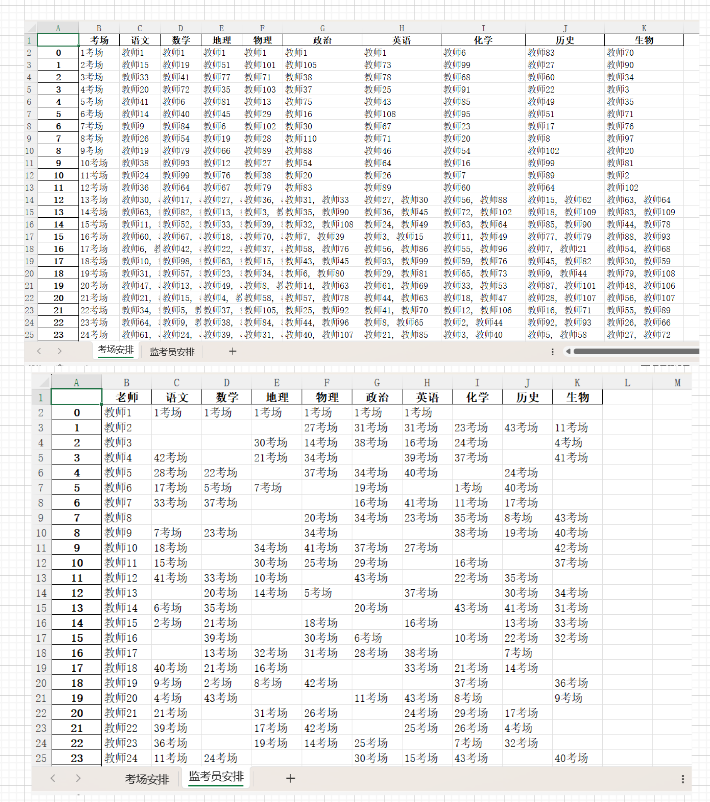
在输出结果这块，做了两个维度的展示。

一个是科目-教室维度
- 展示当前科目、教室下，监考老师的安排
另一个是科目-教师维度
- 展示当前科目，监考老师所在的教室

五、展望

求解是其中的核心，但是在实现这个例子过程中会发现，前置的校验相当重要。如果想做的很完美，则需要在前置校验花费大量的时间，否则求解器抛出个no solution直接傻眼。

基于Python OR-Tools的监考老师任务分配